구조역학 08. 정정구조물의 반력과 부재력 / 전단력 / 모멘트 / 건축기사실기 기출문제

정정구조물의 반력과 부재력

1 .정정구조물의 반력

1) 반력

하중에 대하여 평형상태를 유지하기

위하여 반작용하는 외력

뉴톤의 제3법칙 : 작용과 반작용의 법칙

 

2) 힘의 평행방정식 이용

∑H=0 - 좌우로 움직이지 않는다.

∑V=0 - 상하로 이동하지 않는다.

∑M=0 - 회전하지 않는다.

 

3) 힘의 비례식 사용 방법

( 일상생활에서 )

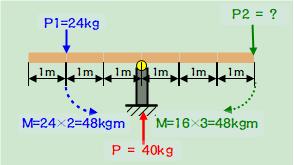
[해설] 

( 구조역학에서 ) 

2. 정정구조물의 부재력(단면력)

외력과 반력 사이에서 버티는

부재내의 힘을 부재력이라 한다.

부재력은 전단력과 휨모멘트,

축방향력 등이 있다.

부재력(응력)을 구하려면

반력을 먼저 구해야 한다.

반력이 0이면 그 부재력도 0이다

2-1. 전단력(shearing force)

1) 정의:

부재의 단면을 재축의 직각방향으로

절단하려는 힘

 

2) 크기 :

임의의 단면에 대한 전단력은

단면의 좌측(또는 우측)에 작용한

모든 외력(반력포함) 중 부재의 축에 대한

직각방향력의 합으로 V또는 S로 나타낸다.

 

3) 부호:

좌측상향, 우측하향(↑↓)일 때 ＋,

좌측하향, 우측상향(↓↑)일 때 －

 

4) 전단력도(S.F.D : shearing force diagram) :

보에서는 (+)일때 상부에,

(-)일때 하부에 그리고

라멘에서는 외측에(+),

내측에 (-)를 그린다.

2-2. 휨 모멘트(bending moment)

1) 정의 :

부재에 작용하는 반력 및 외력에 의해

구부리려고 하는 힘

 

2) 크기 :

임의의 단면에 대한 모멘트의 크기는

단면의 좌측(또는 우측)에 작용한 외력(반력 포함)의

“힘×거리"의 합이며 M으로 나타낸다.

 

3) 부호 :

단면의 좌측에서 생각할 때 시계 방향 (+),

반시계 방향 (-) 로 한다.

( ☞ 단면의 우측에서 생각할 때는 반대로 한다. )

4) 휨모멘트도 (bending moment diagram):

보에서는 (+)일때 하부에,

(-)일 때는 상부에 그리고,

라멘에서는 외측에(＋),

내측에 (－)를 그린다.

2-3. 축방향력(axial force)

1) 정의 :

부재에 재축방향으로 작용하는 힘.

2) 크기 :

임의의 단면에 대한 축방향력은

단면의 어느 한쪽에 작용한 외력(반력 포함)의

축과같은 방향력의 합이다.

3) 부호:

인장력은 ＋, 압축력은 －

4) 축방향력도(A.F.D : axial force diagram) :

보에서는 (+)일때 상부에,

(-)일 때는 하부에 그리고,

라멘에서는 외측에(+),

내측에 (-)를 그린다.