구조역학 06. 트러스의 부재력 / 절점법 / 모멘트법 / 전단력법 / 건축기사 이론 실기

트러스의 부재력

1. 부재력(응력)의 표시방법

1) 응력의 인장(＋)과 압축(­)의 구분은

절점을 향하면(밀면) 압축(­),

절점을 당기면(멀어지면) 인장재 (＋)이다.

 

2) 응력을 구할 때 인장력으로 가정하여

＋이면 가정과 같이 인장력이고

­면 가정과 반대로 압축력이다.

2. truss 응력에 관한 성질

1) 한 직선상에 있지 않는 두개의 부재가 모이는

절점에 외력(P1)이 작용하지 않으면

이 부재의 응력(축방향력)은 0이다.

(P1이 없으면 N₁= N₂= 0)

 

2) 외력(P1)이 한 부재의 방향에 작용하면

그 부재의 응력은 외력과 같고

다른 부재의 응력은 0이다.

(N₁=P1, N₂=0)

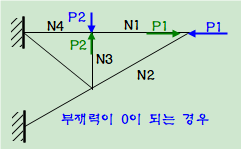
3) 한 절점에 3개의 부재가 모이고

그중 2개가 동일 직선 상에 있고

외력이 작용하지 않을 때(P2=0)

N3=0이며, N1.=N4 이다

 

4) 4개의 부재가 모인 절점 중 2개씩 동일

선상에 있고 외력이 작용하지 않을 때

Na=Nb, Nc=Nd

3. 절점법

1) 반력 :

단순보와 같이 힘의 평형 방정식을 적용한다.

 

2) 부재응력

각 절점에서 작용한 모든 힘

(하중, 지점반력, 부재력)의

H방향과 V방향의 분력의 합은 0이다

. 즉 ∑H = 0, ∑V = 0을 이용한다.

☞ 조건식이 두개이므로 미지의 부재력이

2개 이하인 절점부터 순차적으로 풀어간다.

4. 모멘트법(절단법)

1) 미지의 부재 응력이 3개 이내가 되도록

부재를 절단하여 절단된 부분의 “하중, 지점반력,

절단된 부재응력” 중 미지의 응력이 한 개만 남도록

적당한 점에 ∑M = 0식을 적용하여 푼다.

2) 상현재나 하현재의 응력을 구할 때 사용

상현재 구하기

하현재 구하기

5. 전단력법(절단법)

1) 미지의 부재응력이 2개 이내가 되도록

부재를 절단하여 한 부분의 “하중, 지점반력,

절단된 부재응력”에 대하여

∑V = 0, ∑H = 0의 평형 방정식에 의하여

부재응력을 구한다.

2) 복부재(web)의 응력을 구하는데 쓰인다.